Physically based Jump?

[Paullus]

There has been a lot of talk about jump drives, suggestions going this way and that, attempts to optimize surging on youtube, etc. I am pretty sure that the devs would eventually like to close the chain drive loophole.

I had some musings the other day, and today just ran with it on wolfram alpha. This might be a terrible idea, the most genius idea, or nonsense. It is late in the night for me, and I probably made some errors.

I would like to throw in my two cents on a suggestion that could work:

WARNING: there is a lot of math, if you want my ultimate thoughts, skip to the bottom.

Let us suppose that the jump process is not through the creation of a wormhole, a gate, or a warping of space; it is simply a jump. This means that the tech bypasses special/general relativity, and so we can as well.

The ship must be hurtled at an impressive rate, and then halted at an equally impressive rate. The energy to bring a standstill object to a velocity is:

(1/2)m*v^2, ​

let, v=velocity, m=mass. The energy required to stop is equal; we have then:

m*v^2,​

For the sake of science fiction as well as a requirement of jump modules, let there be an maintenance of efficiency cost:

(m+j)/(m*j)​

Where j=# of jump modules. This form resembles the reciprocal of a reduced mass, such that when j increases the maintenance decreases.

Then we could say that the jump energy of a craft is:

E=m*v^2*[e^(m+j)/(m*j)+1]​

The exponent of this efficiency will quickly go to zero, where added to one provides an easy limit to which jump drives must be added for any sort of practicality.

The advantage of the having energy be linearly proportional to the mass by the velocity squared specifically, is that we could make the velocity configurable, where the max velocity is:

jX{standard velocity}​

which puts another dependence on j again.

Let then P=power which is the ratio of input energy to time. P then has to be:

P=E/t;​

Where t=the time it takes to charge the jump drive. If let P be configurable similarly to v up to a max power of:

jX{standard power} <- (sort of how it works now)​

Then we are free to balance t however we wish. If we say that t is the time in an ideal situation, then let T be the real time, and:

t*b=T;​

where b is a functional factor to find T.

I have two thought experiments we can use to balance and buffer with T
(ignore the random constants, they worked with graphs but could easily change)

1.) the amount of heat buildup on small ships could be devastating, and so a factor of:

[0.6/((e)^(0.002*m-1)(e)^(0.001*j-1))]+1
(x=m,y=j,z=factor)


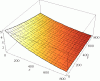
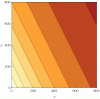
could be applied to t. Note that the topology favors an increase in mass, and so once a ship exceeds a certain mass limit, T is reasonably equal to t.

Again, the balancing is not an issue in this case. We could easily just as well have:



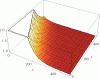
which is a much more drastic hold on mass.

2.) a second maintenance of efficiency can also be applied at this point, with a factor of:

[0.2*m/(j^(3/2))]+1
(x=j,y=m,z=factor)



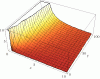
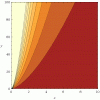
applied to t. Note the exponent on the mass, which favors larger ships in this graph. as the exponent tends towards one, the gradient of the topology becomes linear, and as it leans greater than one, it favors smaller ships. The reason I chose to favor larger ships, was because any reasonable ship can support 5 jump drives. and if we look at the topology extended;



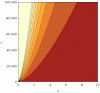
even at an 100,000 mass ship, the affect only matters at j values below ~10. Note the previous maintenance of efficiency becomes practical at ~j=10 as well.


Benefits that may come out of this system:
1. with a calculation of energy that is zero at zero mass, large fighters in that awkward sized zone can become competitive in jumping, while leaving us the ability to still balance the system.
- e.g., the addition of the maintenance of efficiency to the energy, which puts a really simple minimum limit of jump modules depending on the exponent on j.
2. configurable power and velocity outputs (and their respective caps) give players really sweet opportunities to hone their ships.
- e.g., a slow jumping frigate could save a lot on power it needs for alpha damage the second it jumps into battle.
- ... a recon vessel could be created to jump 16 sectors in half a second but optimized with power to not break the ship.
3. fleet carriers (even small ones that carry a few fighters) will be incentivized.
4. chain drives will have to take up huge amounts of space to the point at which a normal jump drive would probably be preferable.

 

[Jojomo]

What speeds do you want them to be able to achieve? Energy costs for anything but the smallest ships will be astronomical.
Will servers be able to handle the planned speeds?

What is the reasoning behind reducing maintenance as j increases?

I know in practice it won't really matter, but I'm curious again: what's the reasoning behind giving larger ships smaller b values than smaller ships?

 

[Paullus]

What speeds do you want them to be able to achieve? Energy costs for anything but the smallest ships will be astronomical.
Will servers be able to handle the planned speeds?

What is the reasoning behind reducing maintenance as j increases?

I know in practice it won't really matter, but I'm curious again: what's the reasoning behind giving larger ships smaller b values than smaller ships?

Energy costs now is already linear (its a little more complicated, it depends on if you have an ideal number of modules, but for huge ships it's all about linear). What this does is make that factor configurable, and doesn't add an initial energy cost. without the initial energy cost, I think it would be easier to balance the model. As I said, the exact numbers can be fidgeted with powers and constants.

Also, the "energy" I gave is the units of energy we use, joules. of course there would be some conversion factor into the units starmade uses, which would be used to balance.

The speed should determine the time it takes to warp, not an actual movement through space.

the maintenance of efficiency is a protection against chain drives. As the number of modules reaches, in this case about 10, at maintenance number is approximately one.

And the first b factor will affect certain ships, but only really small ones. the logic behind this was that it doesn't make sense for tiny ships to be able to warp by themselves, and we can see this in some science fiction. I personally like that idea, because it means for small fighters/drones, we will need carriers. it means you need a big strong ship to survive moving at those velocities.

 

[Paullus]

Hahahahaha I know i'm going to get some hate for this,... but... I was doing some physics reading today, and remembered this post. I looked back through it just now and realized how much work I actually put into this post, so I wanted to see if anyone else had thoughts on it.