"Instant pulses" and some starmade's logic details

[Olxinos]

So, recently i've been toying with logic and more specifically with something i call "instant pulses". I also got the impression that they aren't really well known (along with another rule which might be useful) so i thought that maybe i could make a thread to explain how it works and how to use it.

Let's start with an example:


You might have recognized a Xor (exclusive or, true if its inputs are different) with both inputs (the activation blocks) connected to a button and its output (the Or) connected to a Flip-flop.
Now what will happen if i push the button? Let's name the state of the button B, and the state of the Or-gate R (because O looks too much like 0).
At first glance, R = (A./A) + (/A.A)
(this means R = (A and (not A)) or ((not A) and A), i'll note "and" with ".", "not" with "/" and or with "+")
A./A = 0 (false) hence R = 0 + 0 = 0
So the or gate should always remain false, shouldn't it? Let's try to push that button and see if we guessed right:

Wait. What? Why is the flip-flop on? I didn't even see the Or gate turning on (well this is an image after i press the button so you can't see the Or gate turning on, but if you reproduce the circuit that's what you should get). Obviously this is a bug. Or is it, really?

Introducing time​

There's something we didn't take into account when we analyzed the Xor circuit: how is the signal propagated through the gates?
In fact Starmade seems to behave exactly as if it was a synchronous circuit (except starmade doesn't use an internal clock but we'll come back to that later), this means that the Or gate won't be updated instantly, instead we'll first update the activation blocks then the Not-gates and so on.
So what? Well, let's just reanalyze the circuit:
- i press the button
- the two activation modules turn on (at the same time)
- the two Not-gates turn off, the two And-gates turn on (at the same time)
- the Or-gate turns on, the two And-gates turn off (at the same time)
- the Flip-Flop turns on, the Or-gate turns off (at the same time)
- we wait a fraction of a second before the button turns off
- the two activation modules turn off (at the same time)
- the two Not-gates turn on (at the same time)

Now i reach the good conclusion: the problem came from the And-gates, one of their input was late relatively to the other so for a moment the And-gate turned on but then, they turned off immediately after when the Not-gate signal was eventually propagated.
The And-gates outputed what i call an "instant pulse" (it's not a proper term, but it describes quite well what it is).

Let's say that this behaviour isn't wanted and see if we can "repair" the circuit to avoid this "instant pulse":

Since the problem was just the signal of the Not-gate being late relatively to the signal of the bottom activation block, i just added an activation block between the first activation block and the and-gate to "delay the signal" a bit. Now, it works: the Or-gate never turns on, and the Flip-flop stays off as expected.
(Of course there are other ways to "repair" this circuit, introducing delay blocks for instance)

Practical example: two way counter​

You probably already know about this thing:

This is basically a counter, a decreasing counter actually, the current state can be seen as the binary number 111 (7 in decimal) and if i press the button i get:

110 (6 in decimal)
once again:

101 (5 in decimal)
That's great, but what if i want an increasing counter?
Well actually if i say that on=0 and off=1 instead of on=1 and off=0, i get 000 then 001 then 010, so it can also be seen as an increasing counter.
Okay, but if i want two buttons, an increase AND a decrease one? Now this is less trivial.
Actually there is a really simple solution:

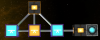
just press that new button and...

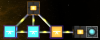
Nice! But why does it work?

Well remember how sending a signal to the rightmost block can be seen as decrementing the counter? Actually sending a signal the middle block can also be seen as decrementing the counter but by 10 (binary) instead of 1, and sending a signal to the leftmost can be seen as decrementing the counter by 100.
So what we're really doing here is decrementing the counter by 111 (7 in decimal) and obviously:
5 - 7 = 6
Wait, let me correct that:
5 - 7 ≡ 6 [8]
Remember that our little counter can only store numbers from 0 (000) to 7 (111), if you try to get a number outside of these bounds, the counter just wraps around (by adding or substracting 8 until you have a valid number if you want, in french we say that "5-7" and "6" are "congrus modulo 8", i don't know how it's called in english).
In general if you have N Flip-flop you make computations modulo 2^N and sending a signal to each Flip-flop can be seen as decrementing by (2^N - 1), here N=3 so 2^3=8 and 2^3-1=7.

Still, we haven't shown that sending all these "substraction signals" at the same time won't mess up the counter yet.
[TODO]

Practical example: Pulse shortener​

Buttons (or delays) already give us relatively short signals, but sometimes you need even shorter, so why not using this small defect of our first Xor circuit at out advantage?

This is a very small and simple circuit, but it can be useful sometimes. Let's see what will happen if i press the button:
- i press the button
- the bottom Flip-flop turns on; the activation module turns on
- the top Flip-flop turns on; the bottom Flip-flop turns off
- a little while later the button turns off
- the activation module turns off
The top Flip-flop is only needed to see the signal here, what is interesting is what the bottom one does: each time you press the button it will send a very short true signal (you can also activate the Flip-flop beforehand so that it will send a very short false signal instead).

Beware of the loop​

When i first toyed with these very short signals, one of my first circuits was the following:

This circuit is a bit more complicated than the previous ones, my intent was to send a pulse each time i received a signal except if that signal caused the last Flip-flop to flip. It works well. But then, i tried to connect the final And-gate to the first flip-flop, so that this circuit would pulse 4 times at each button press (my goal was to make a circuit which could pulse 2^n times with O(log2) blocks) and sadly it doesn't work. But, why?
Well remember when i told you that starmade doesn't use an internal clock to synchronize the logic? This is important now. The thing is: when a block changes its state, starmade tries to reach a stable state for the whole circuit at once. All the tiny steps i described for the previous circuits are followed by starmade in the right order, but he doesn't wait between then: once it finishes a step it immediately starts the next one, but then, when does it stop?
Obviously, starmade can stop if there's no step left, but what if there is always a next step? What if there is an infinite loop in the circuit? Then you have to stop early and that's why this circuit doesn't work.
But, why? This circuit doesn't have an infinite loop, it would only pulse 4 times! That's right, but the game doesn't know that (it could but the only algorithm i know is exponential in the number of logic blocks), all that the game sees is that there is a loop, hence there is an infinite loop possibility.

[TODO]

 

[Megacrafter127]

(by adding or substracting 8 until you have a valid number if you want, in french we say that "5-7" and "6" are "congrus modulo 8", i don't know how it's called in english)

in mathematics, you can simply do (5-7) mod 8 = 6 [mod is the modulo operator], in programming % is the modulo operator.

 

[Olxinos]

in mathematics, you can simply do (5-7) mod 8 = 6 [mod is the modulo operator], in programming % is the modulo operator.

Yup, that's the operation i want to explain, but i don't know how to "read"/"speak" it in english. I mean, if i had to read it, i'd probably say "five minus seven modulo 8" and i guess everybody would understand, but i don't know if it's the proper term.

Edit: i'm concerned by the term because people often confound "modulo" and "remainder of an euclidian divison", but (at least that's how i've learnt it) 5 - 7 ≡ 6 [8] doesn't exactly mean "the remainder of the euclidian division of 5-7 by 8 is 6", the formal definition is:
\exists k \in \mathbb{N}, (5-7) - 6 = 8k
this is different because i can also write 5 - 7 ≡ 30 [8] and that would still be right whereas 30 is obviously not the remainder of the euclidian division, plus % in programming languages might not be exactly the remainder of the euclidian division either (it is for positive numbers, but not for negative numbers)
But maybe that's just me being uselessly pedantic here.

 

[HolyCookie]

Olxinos why has nobody exept me rated this as informative.....
thanks alot, i hate using delays because they aren't really server competitable.
hey just an extra question, would it work to loop an entity on rails of 2 long to measure time?
because the rails are better resistant against server lags and such.

 

[Olxinos]

You mean, creating a clock by detecting the completion of a rail docked entity's movement? (and making it move again each time it completes a movement) Yes of course, that's the principle of the "rotator clock", but you can also do it with rail basics if it's important.

I should complete this topic btw, even though very few people seem to find it usefull x)
In fact, the details i'm talking about aren't relevant for most of the circuits, and even if they are, people tend to just use delays to solve the problem. If you understand well these details though, you can exploit them to make faster, more robust or smaller circuits sometimes.
However, i don't know whether these behaviours will ultimately change or not (not to mention that some gates have surprising behaviours when it comes to "simultaneous instant pulses"), synchronizing with activation blocks should be safe though (i'm thinking of a bit more complex circuits).

 

[HolyCookie]

You mean, creating a clock by detecting the completion of a rail docked entity's movement? (and making it move again each time it completes a movement) Yes of course, that's the principle of the "rotator clock", but you can also do it with rail basics if it's important.

I should complete this topic btw, even though very few people seem to find it usefull x)
In fact, the details i'm talking about aren't relevant for most of the circuits, and even if they are, people tend to just use delays to solve the problem. If you understand well these details though, you can exploit them to make faster, more robust or smaller circuits sometimes.
However, i don't know whether these behaviours will ultimately change or not (not to mention that some gates have surprising behaviours when it comes to "simultaneous instant pulses"), synchronizing with activation blocks should be safe though (i'm thinking of a bit more complex circuits).

i think that what you told is very important for builing huge thing, like a computer.
or for fast things like a movie. the only way i exualy use it is as mini delay, sometimes 2 signals aren't supposed to arrive at the same time, when i use a delay my logic thing (in this case a door) will take about 1-2 seconds longer because of server lag. so what are your plans that you will use this for?

 

[Trekkerjoe]

Awesome. I was working on my insane robotic hand project, and thus far completed the memory storage and retrieval system part thanks to you. I got stuck before because of 'noise' when I selected a memory cell using a T-flip-flop chain. I would temporarily select multiple cells at once. I was able to find a solution based on your findings, using AND gates to make sure the T-flip-flops were updated before I selected a memory cell, significantly reducing lag and completely removing the 'noise'. Thank you.

 

[Plazmatic]

Obviously, starmade can stop if there's no step left, but what if there is always a next step? What if there is an infinite loop in the circuit? Then you have to stop early and that's why this circuit doesn't work.
But, why? This circuit doesn't have an infinite loop, it would only pulse 4 times! That's right, but the game doesn't know that (it could but the only algorithm i know is exponential in the number of logic blocks), all that the game sees is that there is a loop, hence there is an infinite loop possibility.

[TODO]

I don't want to necro, but I felt it useful to correct this. It has nothing to do with a loop going for infinity, having logic go to infinity is not a problem for Starmade, you can make a toggling system that simply continues to infinity for a system, continually flashing lights for example, or counting, or having scrolling letters on a panel of lights.

The problem Starmade is trying to stop is *infinite recursion*. What happens here is that say you have set of logic that feeds into itself with out delays you could have that same system continually try to evaluate logic on itself for infinity and have your server or client become stuck on processing the logic for that system forever if you don't stop it before hand.

Actually, you won't even be able to go forever, because your program will keep track of new variables inside the logic system despite iterating over the same logic, and eventually cause a *stack overflow*, as your program will run out of program stack memory allotted for it using it up with the recursed variables.

Schema as far as I understand could change how the logic system works by converting the recursion to tail recursion and then converting that into a for loop, but he appears to know enough about computer science that he would have done this if it were an option, and even converting it into a for loop wouldn't get rid of process stalling .

 

[AndyP]

There's something we didn't take into account when we analyzed the Xor circuit: how is the signal propagated through the gates?
In fact Starmade seems to behave exactly as if it was a synchronous circuit (except starmade doesn't use an internal clock but we'll come back to that later), this means that the Or gate won't be updated instantly, instead we'll first update the activation blocks then the Not-gates and so on.

Well, starmade is close to that approach.

The starmade logic is "eventdriven"
So hitting a button is sending a "true" signal to all linked gates.
If the target gate changed its state due to that, it will also fire an event to its children.
(We discard packets that do not initiate a change, due to an old looping bug, where a clock kept gathering an additional looping packet every reload.)

Also:
If gate do flip states very fast, they will not be synced to the client.
Especially the "short pulses" you describe, if you send a true followed immediately by a false, it may not be shown to the client at all.

However, every 'event' gets calculated until it hits a certain amount of "changes" to send to the client. If it exceeds a certain limit, it will be paused there, the changes will be synced, and the server will wait until the buffer is empty again. This is used to prevent an update spam to desync clients.

Alltogether, this can lead to some unexpected behaviour like on the XOR, as the update propagates through the gates step-by-step, and different signal travel lenghts (in gate counts) can cause strange issues, especially with flip-flops, that only care for the "false-true" transition to change their state. So sending one input into two networks of logic gates, and comparing the output at the end, has to consider signal travel lenght, or add a delay to the output of the last combination. (delays filter those "short pulses")

So a synchronous circuit would require every gate to have it internal clock, this would be very bad for scaling.
And the Event-based updating allow almost unlimited complexity, while the load put on the computer to show it, is limited to the rendering of blocks. (The server calculates the logic outcome/diff, and sends the update to the client.)

- Andy

 

[nightrune]

Well, starmade is close to that approach.

So a synchronous circuit would require every gate to have it internal clock, this would be very bad for scaling.
And the Event-based updating allow almost unlimited complexity, while the load put on the computer to show it, is limited to the rendering of blocks. (The server calculates the logic outcome/diff, and sends the update to the client.)

- Andy

You could build your own clock gating thing correct? Usually and AND gate, but the delays are usually pretty slow (0.5s).

non-synch logic ----> AND Gate ---> synched data
clock ------------------>

This is actually how it works (at a high level) inside microchips.

 

[AndyP]

Yeah for actual chips this works, however "our" system is event driven, and cant really synchronize data, except you keep a very close eye on signal travel lenght, which is a pain to keep track of in mind once you reach a certain complexity.
And there is no "guaranteed" processing time either, so our logic does not classify for real-time applications and making a clock based on the signal processing chain will be rather impossible. (As the spam-protection randomly adds short delays if the summarized block updates exceed a certain limit.)

However I have seen attempts to build a multiplexer system with the gate timing and have a high compressed signal.
It worked to some extend but was unreliable and had a lot of transmit errors.

- Andy

 

[HolyCookie]

However I have seen attempts to build a multiplexer system with the gate timing and have a high compressed signal.
It worked to some extend but was unreliable and had a lot of transmit errors.

- Andy

Do you know how to uncompress those signals?
You see, I am making this special radar that will track where an enemy is in angles of 45 degrees.
it will translate this information into logic signals, a different signal for each angle (0,45,90,135,180,225,270 and 315)
problem is, instead of giving 1 signal, it will give 2 rapid super compressed on signals too fast to render but a rotor can detect both of them and will rotate twice. I've tried the flip-flop, it works but not always

 

[Olxinos]

I knew I shouldn't have posted or left this unfinished :[
...and I should visit this forum more often...

Plazmatic :
Well yes, I was trying to say that you can't make a retroaction loop in Starmade without a delay block (or some contraption which will delay the signal by a nonzero amount of time like a button, a rotator clock or something like that). As for "infinite recursion", it's another way of telling Starmade would have to loop infinitely because the actual circuit does loop infinitely, so this somehow has something to do with "a loop going for infinity"...
but I think we agree on the fact that without an actual delay of any sort in an oscillator circuit Starmade's logic has to stop the evaluation or stall, which is the point.

The part about stack overflows seems weird though (I find it hard to believe, but I haven't seen the code, so...).
You can perfectly keep track of the state of the circuit and try to reach a stable one with finite and reasonably small memory (depending of the size of the circuit, actually, linear in the number of gates in the circuit) even if the algorithm can't reach a stable state and goes on forever... And if you can do it with finite memory, that's for the better: frequent on the fly memory allocation can be slow, unreliable or both. So why would you do otherwise? (well, of course, only if it doesn't make the code more complex; I don't see how that would be the case here)
Besides, if there really was a (non tail-)recursive call each time a signal caused a connected gate to update, I'm not even sure Starmade could update a circuit made of a couple thousand gates without causing said stack overflow. Recursive functions are usually a bad idea if you know they won't be optimized away and there is a possibly high number of levels of recursion; especially if you can implement it more efficiently with a single loop.

AndyP :
Actually, what I meant when I talked about "Starmade's circuits behaving exactly as if they were synchronous circuits" is that you could expect the output of a Starmade circuit and the output of a synchronous circuit to be the same... as long as loops aren't involved though. Of course, I don't expect the implementation to actually update each gate whenever a clock ticks, as you said, that's pretty inefficient. Nonetheless, I believe Starmade's event-driven system has been implemented with that kind of behaviour in mind so that's why I talked about it.

At the time, I thought the current implementation was probably something resembling a BFS where the root is the first updated block (a button for instance) and you don't visit the neighbouring nodes if the state of the current node hasn't changed (that's the simplest implementation I can think of). I saw some rare behaviours with and/or gates which were inconsistent with those though, so it certainly is a bit different... but this kind of algorithm is otherwise pretty consistent with the description you made of Starmade's logic (set aside the possible interruption caused by the synchronization with the client, I guess that doesn't occur unless the circuit is very big though).