- Joined
- Mar 30, 2014
- Messages
- 44
- Reaction score
- 19
Reading the forums as I do and I came across a post by Sven_The_Slayer in this thread.
http://starmadedock.net/threads/next-generation-advanced-carriers.728/
The important part is how many logic blocks it takes to achieve long timings so as a sort of PSA I would like to introduce you to Coprime Numbers. Two numbers are called coprime if the only factor they share is 1. For example, 2 and 3, 7 and 9, 4 and 11 are all coprime.
So how is this helpful?
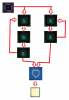
Lets just jump to an example. Starting small lets choose the coprime numbers 2 and 3. We'll create two cyclic groups of timers (meaning the last block activates the first), one 2 blocks long and one 3 blocks long. Now we'll have one more activator block that will activate the first block of both timers. The last thing we need is an and-gate connecting the last block in both groups. Here's a (bad) picture.

With this configuration the light will only be activated when the last block in both groups is active at the same time. This will only happen after the 3 group runs twice and the 2 group runs three times. I can show you this in a table. D is a delay block, 0 is off 1 is on.
DDD|DD
100|10
010|01
001|10
100|01
010|10
001|01
As you can see with the and-gate on the last blocks it will only get activated once every 6 ticks.
So for 6 seconds this isn't too helpful but for longer delays it gets significantly better. For example if you want to delay 60 seconds we'll need to choose two coprime number who's product is as close to 60 as we can get. Luckily 4 and 15 are coprime so we can create two groups, one 4 long and one 15 long. Combing the last blocks of both groups with an and-gate gives us a total of 4+15+1=20 blocks. Pretty good. If we don't need to be so precise we can do three groups one of 2, one of 3, and one of 11. These added with the two and-gates (just run one into the other) gives us a 66 second delay with 18 blocks. So this will be even more effective for longer delays. For example we can get 231 seconds (little less than 4 min) with just three groups 3, 7, 11 and two and-gates for a total of 23 blocks. Beats the pants off of 231 blocks...
Now if you want to take this even further you can reuse the cyclic groups in multiple timers allowing you to have ship clocks with very a long timer but with subdivisions. You could, for example, have a row of plexlights turning off and on with a scrolling pattern of 10010001000001 or whatever set of coprime gaps.
Math.
Aside: If I can get on the dev build I can make a tutorial at some point.
http://starmadedock.net/threads/next-generation-advanced-carriers.728/
The important part is how many logic blocks it takes to achieve long timings so as a sort of PSA I would like to introduce you to Coprime Numbers. Two numbers are called coprime if the only factor they share is 1. For example, 2 and 3, 7 and 9, 4 and 11 are all coprime.
So how is this helpful?
Lets just jump to an example. Starting small lets choose the coprime numbers 2 and 3. We'll create two cyclic groups of timers (meaning the last block activates the first), one 2 blocks long and one 3 blocks long. Now we'll have one more activator block that will activate the first block of both timers. The last thing we need is an and-gate connecting the last block in both groups. Here's a (bad) picture.
With this configuration the light will only be activated when the last block in both groups is active at the same time. This will only happen after the 3 group runs twice and the 2 group runs three times. I can show you this in a table. D is a delay block, 0 is off 1 is on.
DDD|DD
100|10
010|01
001|10
100|01
010|10
001|01
As you can see with the and-gate on the last blocks it will only get activated once every 6 ticks.
So for 6 seconds this isn't too helpful but for longer delays it gets significantly better. For example if you want to delay 60 seconds we'll need to choose two coprime number who's product is as close to 60 as we can get. Luckily 4 and 15 are coprime so we can create two groups, one 4 long and one 15 long. Combing the last blocks of both groups with an and-gate gives us a total of 4+15+1=20 blocks. Pretty good. If we don't need to be so precise we can do three groups one of 2, one of 3, and one of 11. These added with the two and-gates (just run one into the other) gives us a 66 second delay with 18 blocks. So this will be even more effective for longer delays. For example we can get 231 seconds (little less than 4 min) with just three groups 3, 7, 11 and two and-gates for a total of 23 blocks. Beats the pants off of 231 blocks...
Now if you want to take this even further you can reuse the cyclic groups in multiple timers allowing you to have ship clocks with very a long timer but with subdivisions. You could, for example, have a row of plexlights turning off and on with a scrolling pattern of 10010001000001 or whatever set of coprime gaps.
Math.
Aside: If I can get on the dev build I can make a tutorial at some point.
Attachments
-
43.3 KB Views: 170
Last edited by a moderator: