With the new power update just over the horizon, I took some time to do some experimenting in the latest pre-release (200.251), to see if I could deconstruct how the new power system works.
I haven't played much of the dev builds, but from the forums I gathered that long thin reactors seemed to be the best. I used that as a good place to start and try and figure out how power is generated through reactor design. The first question I had was where is the best place to put stabilizers to maximize power output. I built a 3x3x95 long reactor first. Then I placed a few 100x100 stabilizer planes through the xz and xy planes. This allowed me to see where placing my stabilizers would gain me the most stability.

What I noticed was that the amount of stabilization gained depended on the distance from the surface of the reactor not the center of the reactor. I can place a stabilizer 8 blocks away along the z axis and 8 blocks away along the x axis and gain the same amount of stability. I also tested this with a 5x5x5 reactor just to make sure and found a similar result.
Next I wanted to know how stability is gained as a function of distance from the reactor. Is the gain linear as a function of distance, or does it follow a power law with decreasing gains as a function of distance? I built a 1x1x27 reactor. Then perpendicular to the long axis, in the exact center of the reactor rod, I placed one stabilizer block next to the reactor and recorded the percent gain in stability. That is the difference between the stability with the one stabilizer block and without any stabilizer blocks. I then repeated the measurement increasing the distance of the stabilizer block from the reactor one meter at a time. The first 8 meters did not yield an increase in stability. After 8 meters stability grew linearly with distance. After 37 meters no more stability was gained by placing stabilizers further from the reactor. Stability per reactor block is gained linearly until it plateaus at a maximum stability distance, where the maximum stability gained is constant.

I also tested this along the long axis of the reactor and found the same results.
Next I wanted to know where the maximum gain was for different reactor sizes. I started with a long 1x1x11 sized reactor. Below this size there is no need for stabilizers. I placed 1 stabilizer block perpendicular to the long axis and noted the increase in stability. I increased the distance from the reactor until I saw a plateau as in the section above. I recorded the distance in blocks where the plateau occurred. I then increased the reactor size by 2 (1x1x11+2) and repeated the experiment. After a reactor size of 73 blocks gains were slow so I increased the step size by 4 reactor blocks, and at 85 blocks I increased the step size to 10 reactor blocks.
I found that the maximum stability distance best fit a logarithmic function [A*ln(reactor size) + B] where A=27.978 and B =-56.498.

I also recorded the maximum stability gained per stabilizer block above the maximum stability distance. It roughly follows a power law [C *(reactor size)^D] where C=99.527 and D=-1.000.

From this it was easy to calculate the number of stabilizer blocks needed outside the maximum stability distance to achieve 100% stability. The function is roughly linear [E*x+F] where E=1.003 and F=-9.897. It is not necessary to have the same amount of stabilizer and reactor blocks.

There is a bit of a discontinuity at a 85 block sized reactor. This is about where I changed step size so the sampling might not be super accurate. I tested this for a 100 block reactor and found that the prediction to be good to about 1-2 stabilizer blocks.
To summarize the reactor stabilizer relationship I find:
Have fun!
I haven't played much of the dev builds, but from the forums I gathered that long thin reactors seemed to be the best. I used that as a good place to start and try and figure out how power is generated through reactor design. The first question I had was where is the best place to put stabilizers to maximize power output. I built a 3x3x95 long reactor first. Then I placed a few 100x100 stabilizer planes through the xz and xy planes. This allowed me to see where placing my stabilizers would gain me the most stability.
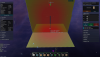
What I noticed was that the amount of stabilization gained depended on the distance from the surface of the reactor not the center of the reactor. I can place a stabilizer 8 blocks away along the z axis and 8 blocks away along the x axis and gain the same amount of stability. I also tested this with a 5x5x5 reactor just to make sure and found a similar result.
Next I wanted to know how stability is gained as a function of distance from the reactor. Is the gain linear as a function of distance, or does it follow a power law with decreasing gains as a function of distance? I built a 1x1x27 reactor. Then perpendicular to the long axis, in the exact center of the reactor rod, I placed one stabilizer block next to the reactor and recorded the percent gain in stability. That is the difference between the stability with the one stabilizer block and without any stabilizer blocks. I then repeated the measurement increasing the distance of the stabilizer block from the reactor one meter at a time. The first 8 meters did not yield an increase in stability. After 8 meters stability grew linearly with distance. After 37 meters no more stability was gained by placing stabilizers further from the reactor. Stability per reactor block is gained linearly until it plateaus at a maximum stability distance, where the maximum stability gained is constant.

I also tested this along the long axis of the reactor and found the same results.
Next I wanted to know where the maximum gain was for different reactor sizes. I started with a long 1x1x11 sized reactor. Below this size there is no need for stabilizers. I placed 1 stabilizer block perpendicular to the long axis and noted the increase in stability. I increased the distance from the reactor until I saw a plateau as in the section above. I recorded the distance in blocks where the plateau occurred. I then increased the reactor size by 2 (1x1x11+2) and repeated the experiment. After a reactor size of 73 blocks gains were slow so I increased the step size by 4 reactor blocks, and at 85 blocks I increased the step size to 10 reactor blocks.
I found that the maximum stability distance best fit a logarithmic function [A*ln(reactor size) + B] where A=27.978 and B =-56.498.

I also recorded the maximum stability gained per stabilizer block above the maximum stability distance. It roughly follows a power law [C *(reactor size)^D] where C=99.527 and D=-1.000.

From this it was easy to calculate the number of stabilizer blocks needed outside the maximum stability distance to achieve 100% stability. The function is roughly linear [E*x+F] where E=1.003 and F=-9.897. It is not necessary to have the same amount of stabilizer and reactor blocks.

There is a bit of a discontinuity at a 85 block sized reactor. This is about where I changed step size so the sampling might not be super accurate. I tested this for a 100 block reactor and found that the prediction to be good to about 1-2 stabilizer blocks.
To summarize the reactor stabilizer relationship I find:
- Stabilizer placement depends on the distance from the surface of the reactor not the center of the reactor.
- Stabilizers placed further away from the reactor than the maximum stability distance all contribute the same gain to stabilization.
- The maximum stability distance depends on the reactor size. It follows a logarithmic function.
- The maximum stability gained per stabilizer block above the maximum stability distance follows a power law with an index of about -1.
- It is not necessary to place the same amount of reactors and stabilizers for 100% stabilization. This value depends linearly on reactor size.
Have fun!

